Why are monads hard?

Jake Woods

What's this talk about?

Monads!

Impossible to explain!

… I'm not going to teach you how to use them.

Instead we're going to figure out why they're so hard to learn.

And maybe help you get started.

So why are they so hard?

Monad is an overloaded term

It refers to lots of concepts

It's like trying to learn "Science"

You need to learn it bit-by-bit

Let's look at some Monads

Monads are: A "Container"?

// Java-ish
List<String>     // Contains many strings
Optional<String> // Contains a string or nothing
Future<String>   // Contains a value from the future

// Scala
List[String]     // Contains many strings
Optional[String] // Contains a string or nothing
Future[String]   // Contains a value from the future

-- Haskell
List String   -- Contains many strings
Maybe String  -- Contains a string or nothing
Async String  -- Contains a value from the future

Monads are: A generic type!

// Java-ish
Monad<A>

// Scala
Monad[A]

-- Haskell
Monad a

Example

// Java-ish
Integer     // Definitely not a Monad
List<A>     // Could be a Monad
Optional<A> // Could be a Monad

// Scala
Int         // Definitely not a Monad
List[A]     // Could be a Monad
Optional[A] // Could be a Monad

-- Haskell
Int         -- Definitely not a Monad
List a      -- Could be a Monad
Optional a  -- Could be a Monad

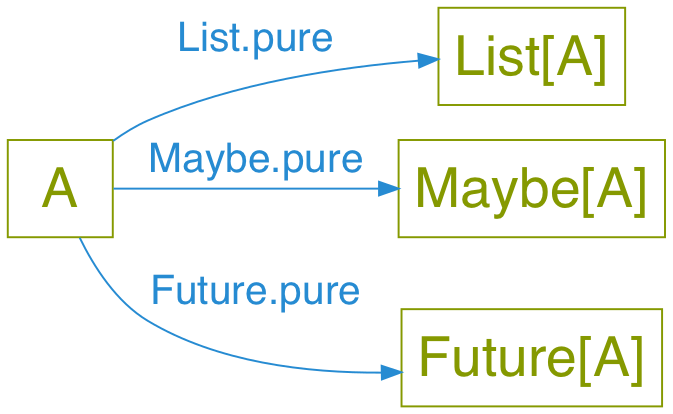
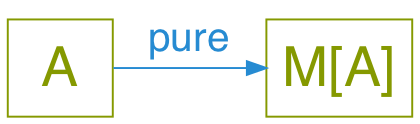
Monads have: pure

// Java-ish
interface Monad<A> {
  static Monad<A> pure(A a);
}

// Scala
def pure(a: A): Monad[A]

-- Haskell
pure :: (Monad m) => a -> m a

It works on Lists!

// Java-ish
List.pure("Hello") == List.of("Hello");

// Scala
List.pure("Hello") == List("Hello")

-- Haskell
pure "Hello" :: List String == ["Hello"]

And Optionals!

// Java-ish
Optional.pure("Hello") == Optional.of("Hello");

// Scala
Option.pure("Hello") == Some("Hello")

-- Haskell
pure "Hello" :: Maybe String == Just "Hello"

And Future!

// Java-ish
Future.pure("Hello") == Future.completedFuture("Hello");

// Scala
Future.pure("Hello") == Future.successful("Hello")

-- Haskell
pure "Hello" :: Async String == CompletedFuture "Hello"

Same interface, different implementation

pure_visual_example_concrete.png

Generalised

pure_visual_example_abstract.png

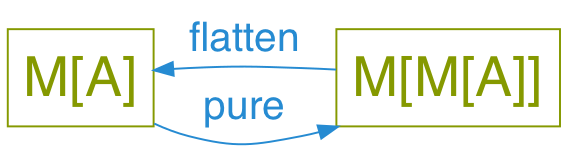
Monads have: flatten

A.k.a join or concat 

// Java-ish
Monad<A> flatten(Monad<Monad<A>> a);

// Scala
def flatten(a: Monad[Monad[A]]): Monad[A]

-- Haskell
concat :: (Monad m) => m (m a) -> m a

Like Lists

// Java-ish
List.of(List.of(1,1), List.of(2,2)).flatten
  == List.of(1,1,2,2);

// Scala
List(List(1,1), List(2,2)).flatten == List(1,1,2,2);

-- Haskell
concat [[1,1],[2,2]] == [1,1,2,2]

Or Optionals!

// Java-ish
Optional.of(Optional.of("Hi")).flatten
  == Optional.of("Hi");
Optional.of(Optional.empty).flatten
  == Optional.empty;

// Scala
Some(Some("Hi")).flatten == Some("Hi")
Some(None).flatten == None

-- Haskell
concat Just (Just "Hi") == Just "Hi"
concat Just Nothing == Nothing

Or Futures

// Java-ish
Future.of(Future.of("Hello")).flatten
  == Future.of("Hello");

// Scala
Future.successful(Future.successful("Hello")).flatten
  == Future.successful("Hello")

-- Haskell
concat (Async (Async "Hello")) :: Async (Async String)
  == (Async "Hello")

Same interface, different implementation

flatten_example_concrete.png

Generalised

flatten_example_abstract.png

Monads are: A type that can be nested

nesting_example.png

Monads are: A type that can be arbitrarily nested

nesting_example_pure_and_flatten.png

Monads have: flatMap

Also known as bind or >>= 

// Java-ish
interface Monad<A> {
  Monad<B> flatMap(Function<A, Monad,B>> fn);
}

// Scala
trait Monad[A] {
  Monad[B] flatMap(fn: A => Monad[B]): Monad[B]
}

-- Haskell
bind :: (Monad m) => m a -> (a -> m b) -> m b

Example

[1,2,3].flatMap(a => [a, a])
// Returns [1,1,2,2,3,3]

Maybe(1).flatMap(value => Some(value+2))
// Returns Maybe(3)

Maybe(1).flatMap(value => None)
// Returns None

flatMap using map and flatten

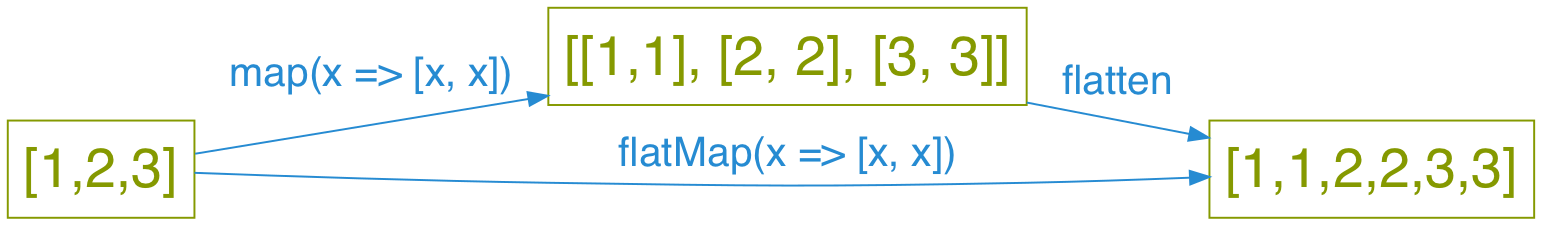
list_flatMap_example.png

Generalised

flatmap.png

Also known as bind

-- >>= is pronounced bind in Haskell. Wat!
[1,2,3] >>= \a -> [a, a]
-- Returns [1,1,2,2,3,3]

Just 1 >>= \value -> Just (value+2)
-- Returns Just 3

Just 1 >>= \value -> Nothing
-- Returns Nothing

Monads can: be used with For/Do

// Scala
for {
  a <- Some(5)
  b <- Some(10)
} yield a + b
// Returns: Some(15)

-- Haskell
do
  a <- Just 5
  b <- Just 10
  pure a + b
-- Returns: Just 15

Monads are: A way of composing certain types of functions

Normal Function Composition

// Java-ish
Function<String, String> toUpperCase = ...;
Function<String, String> trim = ...;
Function<String, String> toUpperCaseAndtrim =
  toUpperCase.compose(trim);

// Scala
def toUpperCase(input: String): String = ...
def trim(input: String): String = ...
def toUpperCaseAndTrim = toUpperCase.compose(trim)

-- Haskell
toUpperCase :: String -> String
trim :: String -> String
toUpperCaseAndTrim = toUpperCase . trim

Monadic Function Composition

// Java-ish
Function<String, Promise<String>> toUpperCase = ...;
Function<String, Promise<String>> trim  = ...;
Function<String, Promise<String>> toUpperCaseAndTrim =
  toUpperCase.monadCompose(trim);

// Scala
def toUpperCase(input: String): Promise[String] = ...
def trim(input: String): Promise[String] = ...
def toUpperCaseAndTrim =
  monadCompose(toUpperCaseService, trimService)

-- Haskell
toUpperCase :: String -> Promise String
trim :: String -> Promise String
toUpperCaseAndTrim = toUpperCase >=> trim

Monads are: Something to do with Sequential Computations?

In most languages sequence is implied: 

def main() = {
  // Executes doA then doB then doC and then returns
  val a = doA();
  val b = doB();
  val c = doC();
  a + b + c
}

But in some languages that isn't the case

-- Executes in an arbitrary order as everything is lazy
main =
  let a = doA
      b = doB
      c = doC
  in a + b + c

Monads imply sequential computation

-- Executes doA then doB then doC and then returns a result
main = do
  a <- doA
  b <- doB
  c <- doC
  pure a + b + c

Monads are: Something for managing side effects?

In some languages we can freely mix side-effects into normal code:

// Java-ish
Integer add(Integer a, Integer b) {
    System.out.println("Hello World!");
    return a + b;
}

// Scala
def add(a: Int, b: Int): Int = {
  println("Hello World!")
  a + b
}

But not in all languages

add :: Int -> Int -> Int
add a b = do
  println "Hello World" -- ERROR! Doesn't compile
  a + b

Instead we have to mark side effecting functions with a type

add :: Int -> Int -> IO Int
add a b = do
  println "Hello World" -- Compiles
  pure $ a + b

flatMap lets us compose that type.

And we get flatMap from Monad!

They're all Monads!

No wonder they're so hard to learn…

Something something Laws

  • There are rules defining how Monads must be implemented
  • Mostly it's about making them act in a sane way
  • They're outside the scope of this talk

But wait! There's more!

We need to talk about Maybe/List/Promise/Reader/Writer/State/IO

Well…

They are Monads!

But that's the boring bit about them.

Each of those types do something unique and valuable!

They enrich a type to give it extra functionality

  • Maybe adds null
  • List adds multiple values
  • Promise adds asynchrony
  • Reader adds dependency injection
  • Writer adds logging
  • State adds arbitrary state
  • IO adds the ability to use the computer

This has nothing to do with Monads!

Example

// Java-ish
Integer value;          // A boring integer
List<Integer> values;   // An exciting bunch of integers!
Future<Integer> value;  // An exciting asynchronous integer!

// Scala
value: Int;          // A boring integer
values: List[Int];   // An exciting bunch of integers!
value: Future[Int];  // An exciting asynchronous integer!

-- Haskell
value :: Int         -- A boring integer
values :: List Int   -- An exciting bunch of integers!
value :: Async Int   -- An exciting asynchronous integer!

You have to learn each one individually, Monads won't help you here!

Then why should I care if they're Monads?

They're all Generic types

// Java-ish
Maybe<T> List<T> Promise<T> Reader<T>
Writer<T> State<T> IO<T>

// Scala
Maybe[T] List[T] Promise[T] Reader[T]
Writer[T] State[T] IO[T]

-- Haskell
Maybe t, List t, Promise t, Reader t
Writer t, State t, IO t

We want to compose them…

Monads help us compose generic types!

They're a Design Pattern for a specific type of composition.

When I say "X is a Monad" I know:

  • This type is generic
  • This type enriches normal types with extra behavior
  • I can compose this type using flatMap/bind
  • I can compose this type using For/Do comprehension

It's a design pattern!

Learn once, write everywhere!

In Summary

A Monad implies a whole bunch of things

Try to learn them a little bit at a time!

It's ok to be overwhelmed!

This stuff takes time to learn.

Extra Reading

Thanks!

Questions?

mindblown.gif